Một thuật toán từng bị xem là chậm... và cú “phản đòn” ngoạn mục của nó

Beo

21 Th10 2025 — 5 min read

Có những nhận định và kiến thức được truyền bá rộng rãi khiến nhiều người nghĩ rằng chúng chỉ có thể là như vậy.

Trong những số đó là một thuật toán được sử dụng để implement cơ chế thay thế cache khi bể cache đầy: LFU cache (Least Frequently Used) chỉ có thể đạt được average-case time complexity là O(log n) vì thuật toán này phải sử dụng một cây min-heap. Điều này đã được chấp nhận suốt nhiều năm, khiến nhiều developer chọn LRU (Least Recently Used) với average-case time complexity là O(1) thay vì LFU cho dù LFU phù hợp hơn cho use case của họ.

🔍 Tại sao lại là min-heap?

Bài toán cốt lõi là:

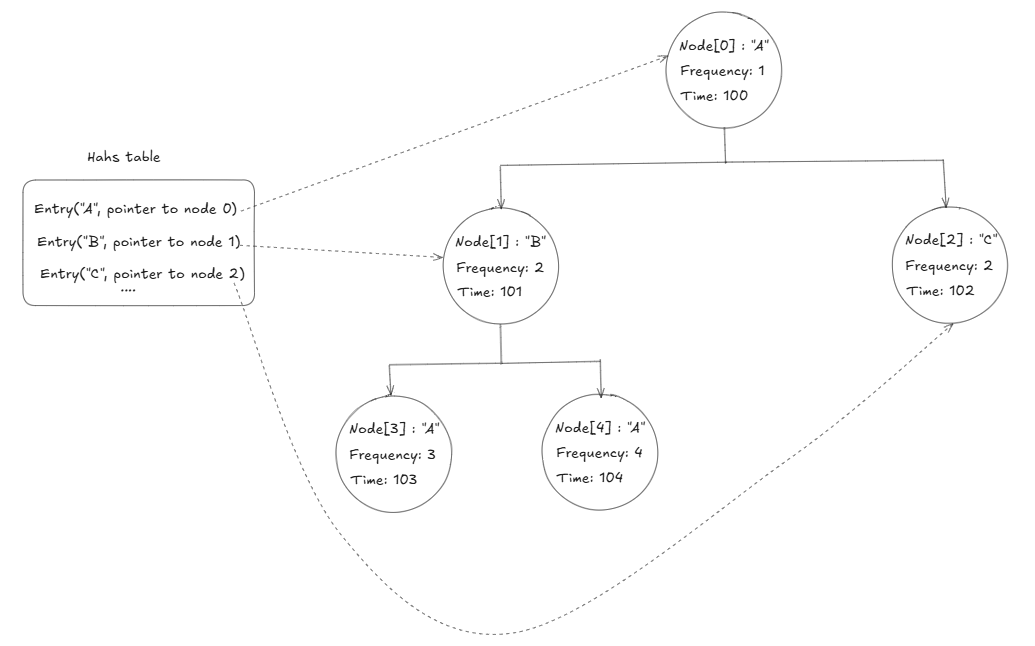
Khi cache đầy và ta cần thêm một phần tử mới vào cache, làm sao tìm được phần tử có tần suất truy cập thấp nhất một cách nhanh nhất để loại bỏ nó khỏi cache và nhường chỗ cho phần tử mới? Cây min-heap trở thành lựa chọn vì tính chất của nó là luôn giữ phần tử nhỏ nhất (tần suất thấp nhất) ở root node nên việc xác định phần tử cần loại chỉ mất O(1).

Cách làm truyền thống với min-heap:

Hãy tưởng tượng bạn là một thủ thư và trên bàn làm việc của bạn có một chồng sách top 10 cuốn sách hay được mượn, quy tắc để quản lý chồng sách chỉ có 10 cuốn đó của bạn là “luôn loại bỏ cuốn sách ít được mượn nhất để thay thế khi có một cuốn sách mới nổi lên lọt vào top 10”. Bạn sẽ sắp xếp tất cả sách thành một kim tự tháp, với sách ít được mượn nhất luôn đặt ở đỉnh tháp để lúc nào cũng có thể lấy nó ra ngay lập tức.

Mỗi khi có người mượn một cuốn sách bất kỳ, bạn cập nhật lại số lần được mượn của cuốn sách đó, rồi sắp xếp lại toàn bộ kim tự tháp để đảm bảo cuốn có tần suất truy cập thấp nhất vẫn ở đỉnh. Quá trình sắp xếp lại này gọi là rebalancing, bạn sẽ phải so sánh và hoán đổi vị trí nhiều cuốn sách từ đỉnh xuống đáy hoặc ngược lại, nên sẽ có time complexity là O(log n).

Điều tồi tệ nhất là việc rebalancing không chỉ xảy ra mỗi khi bạn thực hiện thay đổi tần suất truy cập cho một cuốn sách (access), mà nó sẽ xảy ra ngay cả khi bạn thực hiện loại bỏ cuốn sách có tần suất được mượn thấp nhất (deletion), hay kể cả sau khi loại bỏ và có một cuốn sách mới được thêm vào để thế chỗ cuốn sách đã bị loại bỏ (insert). Đó là lý do tại sao LFU bị "kẹt" ở O(log n).

Cho đến năm 2010, một nhóm nghiên cứu gồm Giáo sư Ketan Shah, Anirban Mitra và Dhruv Matani đã cho ra đời một technical report "An O(1) algorithm for implementing the LFU cache eviction scheme” (paper được đăng tải chính thức trên arXiv năm 2021).

💡 Điều đặc biệt ở đây là gì?

Họ đã tạo ra một cách thông minh hơn để implement thuật toán sử dụng Hash Table và các Doubly Linked List. Cách implement này đã giúp thuật toán LFU có thể đạt average-case time complexity là O(1).

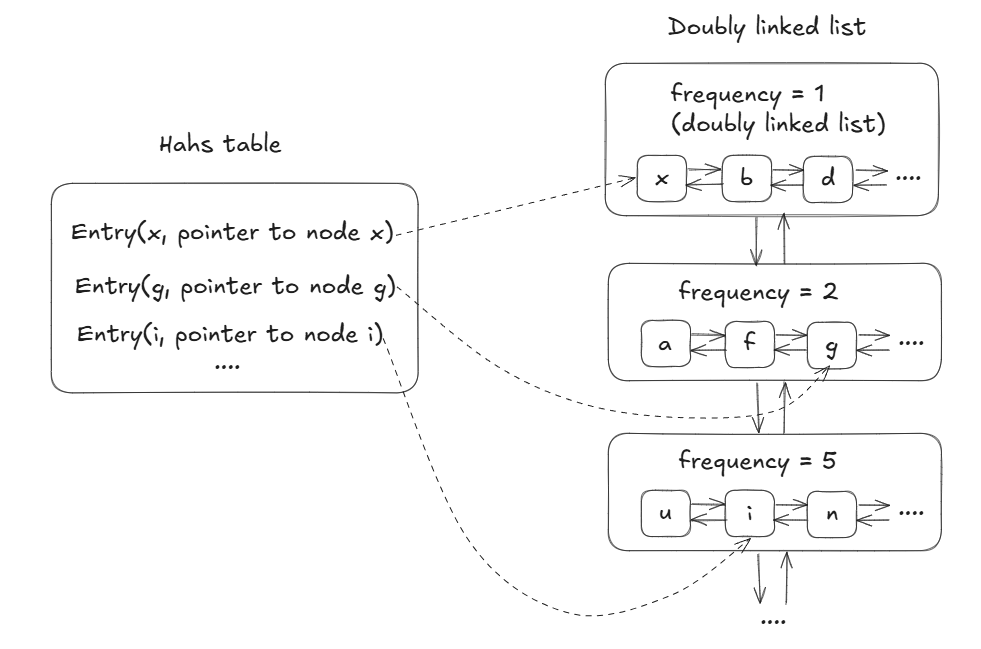
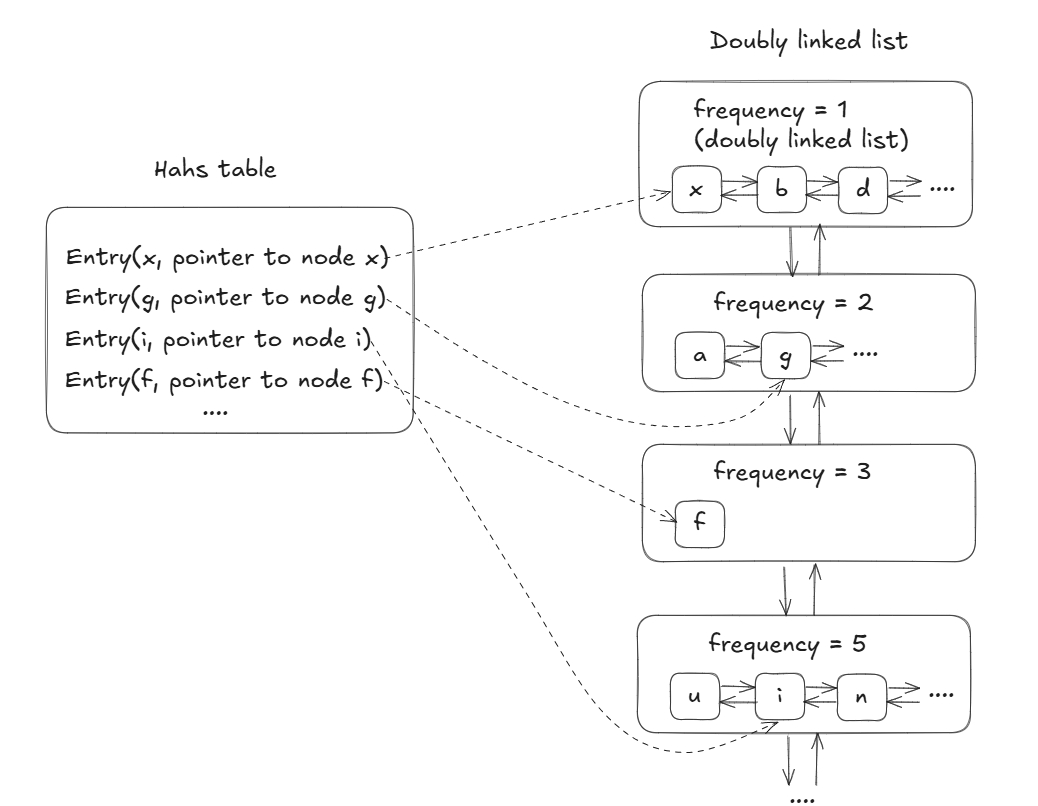
Đột phá của giải pháp O(1) nằm ở việc họ hoàn toàn thay đổi cách impement thuật toán. Thay vì một kim tự tháp dọc, họ tạo ra các kệ sách ngang (mỗi kệ là một Doubly Linked List). Mỗi kệ chứa tất cả sách có cùng số lần được mượn. Kệ đầu tiên chứa sách mượn 1 lần, kệ thứ hai chứa sách mượn 2 lần, và cứ thế. Các kệ này được liên kết với nhau bằng Doubly Linked List, và một hash table giúp bạn tìm ngay vị trí của bất kỳ cuốn sách nào trong chớp mắt.

Khi có người mượn một cuốn sách đang ở kệ 1, sau này bạn chỉ cần chuyển nó sang lưu trữ tại kệ 2 là đã cập nhật được số lần cuốn sách được mượn, một thao tác đơn giản không cần sắp xếp lại gì cả. Khi cần loại bỏ, bạn chỉ việc lấy cuốn đầu tiên trên kệ đầu tiên. Mọi thao tác đều là di chuyển trực tiếp, không cần so sánh hay sắp xếp, do đó đạt được time complexity là O(1).

Và tất nhiên, không có thuật toán nào là hoàn hảo, để đạt được cái này chúng ta cần phải chấp nhận đánh đổi một cái khác.

Cách tiếp cận mới của giáo sư Ketan Shah cũng cần một số sự đánh đổi trong các phương diện khác:

Việc sử dụng cách tiếp cận mới sẽ phải tốn nhiều bộ nhớ của RAM hơn để quản lý hash table và các Doubly Linked List.
Cách tiếp cận này cũng khó implement, khó maintain hơn so với cách truyền thống.

🎯 Bài học cho chúng ta:

Trong thế giới công nghệ đang thay đổi chóng mặt, đừng bao giờ chấp nhận một giới hạn chỉ vì "mọi người đều nói vậy". Những gì được coi là "tối ưu nhất" hôm nay có thể sẽ bị phá vỡ vào ngày mai bởi một ý tưởng sáng tạo.

Đối với các developer thế hệ mới: